Plots Level

1. Contour Plot Level Sets
2. Plow Tool
3. Square
4. How To Plot Level Curves Of F(x,y) = 2x^2 + 5y^2. F(x,y) = C ...
5. Plot Level Curves
6. Plots Significance Levels

Oct 16, 2019 Scatter plots’ primary uses are to observe and show relationships between two numeric variables. The dots in a scatter plot not only report the values of individual data points, but also patterns when the data are taken as a whole. Identification of correlational relationships are common with scatter plots. A plot device is a means of advancing the plot in a story. It is often used to motivate characters, create urgency, or resolve a difficulty. This can be contrasted with moving a story forward with dramatic technique; that is, by making things happen because characters take action for well-developed reasons. You can have a maximum of maximum total of one-hundred (100) Super Plots per farm. FarmVille gives you the first (1 st) four (4) Super Plots for free, on a farm. You can purchase up to ninety six (96) additional Super Plots for a maximum total of one-hundred (100) Super Plots on your farm. May 03, 2010 A level plot is a type of graph that is used to display a surface in two rather than three dimensions – the surface is viewed from above as if we were looking straight down and is an alternative to a contour plot – geographic data is an example of where this type of graph would be used. A contour plot uses lines to identify regions of different heights and the level plot uses coloured regions to produce a similar effect.

As we've already seen, it is often times very difficult to graph surfaces in $mathbb{R}^3$ on a flat surface. However, we will develop a method of depicting a surface given by a two variable real-valued function $z = f(x, y)$.

From the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the $xy$-axis and the surface generated by the function $z = f(x, y)$.

For example, consider the two variable real-valued function $f(x, y) = x^2 + y^2$, which represents a paraboloid that is parallel to the $z$-axis, and consider the level curves generated by the intersection of this paraboloid with the planes $z = 1$, $z = 2$, and $z = 3$. These level curves will be concentric circles with center $(0, 0)$. The image below depicts the level curve of this paraboloid corresponding to $z = 2$.

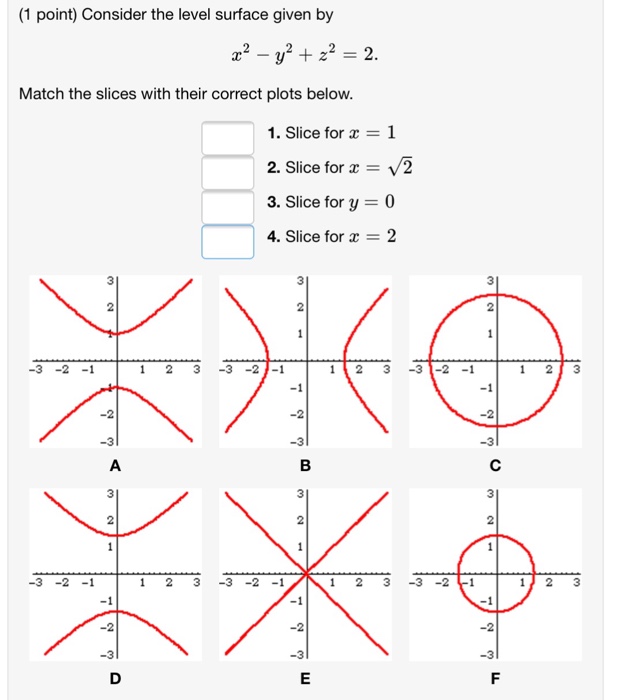
Another example is the two variable real-valued function $f(x, y) = x^2 - y^2$ which represents a hyperboloid. The level curves generated by the planes $z = 1$, $z = 2$, and $z = 3$ are hyperbolas. The image below depicts the level curve of this hyperboloid corresponding to $z = 1$.

Contour Plot Level Sets

We will now look at another definition is applying these level curves.

When we depict a contour plot of a two variable function, it is important to note that it is impossibly to place all the level curves of $z = f(x, y)$ onto the $xy$-plane, and so we often choose specific level curves. For example, consider the paraboloid $f(x, y) = x^2 + y^2$ once again. We saw above that the level curves for $f$ were concentric circles. The following image represents a few planes that are parallel to the $xy$-plane intersecting this paraboloid.

If we project all of these level curves onto the $xy$-plane, then we would obtain the following contour plot for $f(x, y) = x^2 + y^2$.

For a two variable real-valued function, a contour plot can tell us regions of elevation and regions of depression. For example, from above, we can see that as $x$ increases, we scale up the paraboloid. The same happens for when $y$ increases. However, when both $x$ and $y$ approach $0$, we get closer and closer to the part of the paraboloid that is at its 'deepest'.

Example 1

Describe the shape of the surface given by the following contour plot:

We first note that the elevation increases as we go along the $x$-axis in both directions, and that the elevation decreases as we go along the $y$-axis in both directions. We also note that the level curves of this contour plot are hyperbolas. We deduce that this is a contour plot of a hyperboloid.

Example 2

Plow Tool

Construct a contour plot for the surface generated by the two variable real-valued function $f(x,y) = x + 2y$.

We first note that $f$ represents a slanted plane. Let's now determine what the level curves of $f$ look like. First let $z = 0$. Then we get the equation $0 = x + 2y$, or rather $y = -frac{x}{2}$, which represents a negative straight line. In fact, notice that the level curve corresponding to $z = k$, $k in mathbb{R}$ is $y = -frac{x}{2} + frac{k}{2}$ which represents a negative straight line. Thus, all of our level curves are straight lines. Notice that as $k$ increases, the $y$-intercept of the corresponding level curve also increases, and so we can even determine the relative elevation of the plane as depicted with the contour plot for $f$ shown below:

Box-and-whisker plot worksheets have skills to find the five-number summary, to make plots, to read and interpret the box-and-whisker plots, to find the quartiles, range, inter-quartile range and outliers. Word problems are also included. These printable exercises cater to the learning requirements of students of grade 6 through high school. Grab some of these worksheets for free!

Analyze the data sets with single-digit, 2-digit, and 3-digit values, and jot down the five key values: the 1st, 2nd, and 3rd quartiles, and minimum and maximum that constitute the 5-number summary.

Level up identifying the upper and lower quartiles, maximum and minimum values, and median, necessary to make box and whisker plots, from data sets involving decimal values.

Constructing box plots is the next step when you’re ready with your five-number summary. Plot the five values on the graph, and create the box plot to represent the given sets of data.

Climb up the ladder in making box plots with these worksheets! Observe the data sets that involve more than 10 data values and also decimals, figure out the elements of the box plot, and create it.

Read the given data carefully and determine the five-number summary to make box-and-whisker plots. Each pdf worksheet has three problems.

Dig into practice with these handouts for 6th grade and 7th grade students. Read the scenarios and interpret the box-and-whisker plots to answer the word problems based on the five-number summary.

These pdf worksheets for grade 7 and grade 8 have exclusive word problems to find the five-number summary, range and inter-quartile range.

For the given data, make a box-and-whisker plot. Interpret the data to find Q1, Q2, Q3, maximum and minimum values.

Square

Each printable worksheet has eight problems in store for 8th grade and high school students. Find the outliers by computing the quartiles and the inter-quartile range.

How To Plot Level Curves Of F(x,y) = 2x^2 + 5y^2. F(x,y) = C ...

Related Worksheets

Plot Level Curves

»Mean

Plots Significance Levels

»Mean, Median, Mode and Range